Emma Moore

These are my summary notes based on reading the book But How Do It Know? by J. Clark Scott. If I’ve used any other resources, I’ll link them where appropriate. Part 1 is an introduction to logic gates.

Logic Gates

Logic gates are small electrical circuits wired in such a way as to process binary inputs into a binary output. To do this, they use transistors, which are basically electronic switches that can be turned on or off.

I’ll only show a couple of the electrical circuits, since it’s not necessary to understand the electronics to understand how the gates are used to build a computer. I think the AND gate is one of the easiest to understand.

AND gate

AND gate electrical circuit:

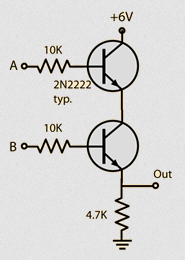Hyperphysics

The above can be simplified into the following diagram:

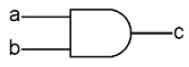But How Do It Know?

For C to be on, A and B must both be on. Any other combinations will result in C being off:

A	B	C
0	0	0
0	1	0
1	0	0
1	1	1

NAND gate

A NAND gate is so named because it is a negative AND gate. So the C output will be the opposite of an AND gate. Inputs A and B must both be on for the output, C, to be off.

Electrical circuit:

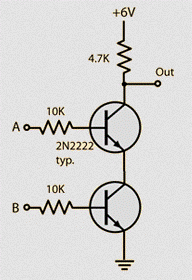Hyperphysics

Simplified diagram:

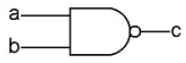But How Do It Know?

Possible combinations:

A	B	C
0	0	1
0	1	1
1	0	1
1	1	0

Gates can be combined to create other types of gates:

An AND gate can be created by combining a NAND gate with a NOT gate:

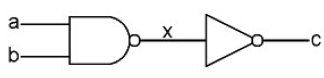But How Do It Know?

An OR gate can be made by combining two NOT gates with a NAND gate:

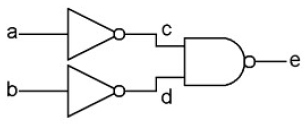But How Do It Know?

A XOR gate can be made by combining two NOT gates with three NAND gates.

But How Do It Know?

Let’s look at one combination for the XOR gate (the second row in the table below):

• When A is off, C will be on (NOT gate)
• When B is on, D will be off (NOT gate)
• When A is off and D is off, F will be on (NAND gate)
• When B is on and C is on, E will be off (NAND gate)
• When E is off and F is on, G will be on (NAND gate)

A	B	C	D	E	F	G
0	0	1	1	1	1	0
0	1	1	0	0	1	1
1	0	0	1	1	0	1
1	1	0	0	1	1	0

You can start to see how logic gates can be combined in various ways to start building out a computer. However, these gates can also be made directly with transistors, which is much more efficient for building modern computers. Here’s a transistor OR gate, which is a bit simpler than combining two NOT gates and a NAND gate:

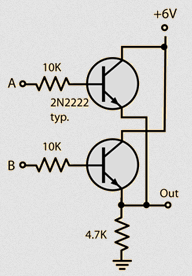Hyperphysics

Summary

Here are the simplified diagrams of the main gates discussed in But How Do It Know?:

AND	NOT	NAND

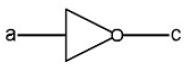OR	XOR

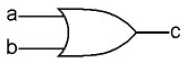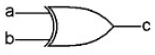To start building the parts that make up a computer, these gates can be connected in various ways to create more complicated logic.

In part 2, I’ll go through an example from But How Do It Know? that shows how NAND gates can be combined to make computer memory.